|
0 Comments
This is a picture of the problem (which is similar to the Snack Bag problem): And this is what the solution looks like:
Prime Time Study Guide Test-Monday, Sept. 21 and Tuesday, September 22
It is a BIG test. It is worth 100 points. You need to know your multiplication facts, know a prime number, and you must know the difference between factors of a number (factors are always smaller than the number, factors are what you multiply to get that product) and multiples of a number (multiples are that number or larger, they are what you get when you multiply the number by 1, 2, 3, 4, etc.). You must be able to:
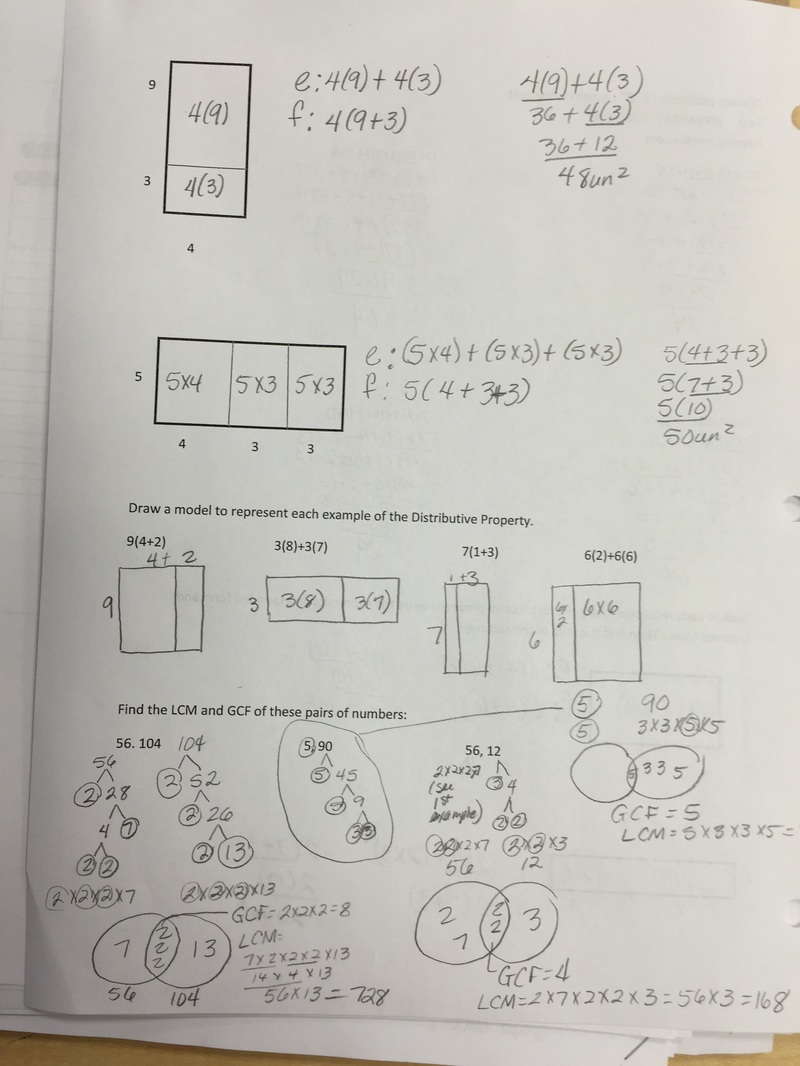
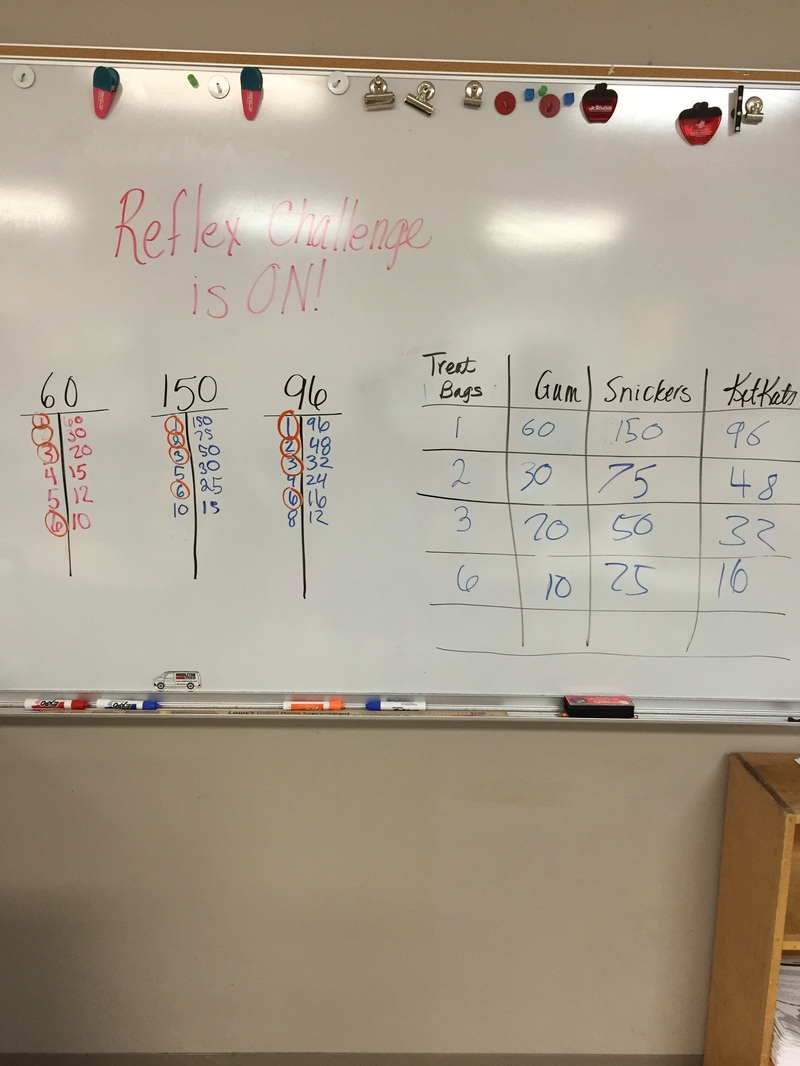
5. If you eat oatmeal every 5 days, a hamburger every 7 days, and yogurt every 3 days, if you had all three today, how many days until you have all three again (you must find the LCM of 3 numbers). 35 days. Show how you work. I would list multiples of the numbers. 5 7 3 5 7 3 10 14 6 15 21 9 20 28 12 25 35 15 30 42 18 35 49 21 40 56 24 45 63 27 30 33 35 7. 32 42 2 x 16 2 x 21 2 x 8 3 x 7 2 x 4 2 x 2 Remember, in real class, you ALWAYS circle the prime numbers. Here I had to highlight them. So the factor string for 32 is 2 x 2 x 2 x 2 x 2 42 is 2 x 3 x 7 I CAN’T GET MY VENN DIAGRAM TO WORK. YOU HAVE EXAMPLES IN YOUR BINDER. So a 2 is in both factor strings and one 2 would go into the exclusive GCF club (Greatest Common Factor Club), or shared part of the circles. Four 2s would go into the circle for 32 only. 3 and 7 would go into the circle for 42. The GFC is everything inside the shared part multiplied, this time it is only 2. The GCF of 32 and 42 is 2. The LCM (Least Common Multiple) is found by multiplying ALL the digits in both circles (including the shared portion), or 2x2x2x2(from the 32 circle only)x2(from the shared part)x3x7(from the 42 circle only) (which is 32 x 3 x 7 = 672). So the LCM of 32 and 42 is 672. 8. Remember: Parenthesis Exponent Multiplication Division Addition Subtraction - I’ll highlight each step I’m doing 6 (3+2) - 4 4 + (2-1) x (2+2) 6 x 3 - 4(2) / 2 6(5) - 4 4 + 1 x (2+2) 18 - 4(2) / 2 30 - 4 4 + 1 x 4 18 - 8 / 2 26 4 + 4 18 - 4 8 14 Always do ONE step at a time. Prime factorization (and factor strings) are all about breaking a number down into the prime numbers (or for factor strings, any combination of possible factors to create a product) that make up a number. An example: 30 is a composite number. It can be made in any number of ways 1 x 30, 2 x 15, 3 x 10, 5 x 6 OR 2 x 3 x 5. With larger composite numbers (like 240), there are many more possibilities (like 2 x 120, 2 x 12 x 10). I told them prime factorization is like taking a Lego model apart into all its little pieces.
The picture below shows what they are doing for bellwork this week. It is practicing Order of Operation skills. Since they will be moving into Algebra within a few years, I make them show all the steps they use (GOOD HABITS START EARLY). These are rectangles that show all the factor pairs for the numbers 1-30. All three classes worked on a set for their classes. Here's what we discovered:
Prime numbers only have two rectangles, because they only have 1 and the number as factors. Some numbers make square rectangles, but only special numbers like 4, 9, 16, and 25. That's because they are created when you multiply a number by itself (like 2 x 2 = 4). These numbers have an odd number of rectangles that can be made. These are called Square numbers (one of their factor pairs creates a square). Most numbers have an even number of rectangles (like 21 has 1 x 21, 21 x 1, 3 x 7, and 7 x 3). Numbers that have more than themselves and one as factors are known as Composite numbers. We have also been practicing applying the rules of divisibility. The unit begins with understanding factors, products, divisors, and how these numbers are related. Knowing their multiplication facts is assumed as we start the unit. To brush up on those facts (and to learn strategies for earning points), we played The Factor Game last week. If you haven't played it with your student, please do very soon.
This week will include The Product Game. Both games allow the student to think about how factors and divisors are just different ways of looking at what makes a number. Example: 2 x 5 = 10. 2 and 5 are factors of 10 (they can be multiplied together to find the product 10), but they are also divisors of 10. You can divide 10 by 2 or by 5 and get a whole number as the answer. 2, 5, and 10 also make a multiplication and division fact family. We have also talked about: PRIME numbers - numbers that only have 1 and the number itself as factors/divisors (5 is a prime number). COMPOSITE numbers - numbers that have more factors or divisors than just themselves and 1 (10 is a composite number with factors of 1, 2, 5, 10). SQUARE numbers - numbers like 4 and 9, which can be modeled with tiles to make a perfect square (2 x 2, 3 x 3). These will all be on their first quiz, which is Thursday (8/27/15). Some problems on the quiz will require them to identify each kind of number and explain (with words) how they know. The students are comfortable with how to find the mean of a set of data. Add all the data values together and divide by the number of values. The other name for the mean is the average. I am seeing problems with them not double checking their work, therefore they make careless errors. I always tell them to add the set of numbers twice. If you get the same answer two times in a row, the chances are you added correctly. They are allowed to use a calculator.
What is the MAD (mean absolute deviation)? First, you have to find the mean of the data set. Then, you notice that some numbers in the data set can be the same as the mean, but some numbers are not the same as the mean. This is what the MAD examines. To find the MAD, you have to first find out how far each data value is from the mean. So you subtract the mean from the data value (or the difference or how much it DEVIATES from the mean). SOMETIMES, this is a negative number, but we find the absolute value of each difference (a numbers' absolute value is always positive; it tells how far from zero the number is). After finding the positive value of each difference, you add these together and divide by how many numbers you just added (it's finding the average again). This is the average of how far those numbers NOT exactly the mean are different from the mean (or the mean absolute deviation). In the picture below, you can see not only how we found the MAD, but the it identifies the five number summary as well. The data set used: 10, 15, 20, 22,22, 26, 30, 31, 35, 40. Our unit is all about data and statistics (what it really tells us and how to gather it and display it). Today (thanks to NC for the tip), I'll be teaching them a song about what each thing means. We will be taking more notes, getting more examples, and practicing how to find these things.
The song lyrics go to the tune of "Hey Diddle, Diddle, the Cat and the Fiddle" of nursery rhyme fame. The lyrics: Hey diddle diddle, the Median's the middle; You add then divide for the Mean; The Mode is the one you see the most; And the Range is the difference between. I would love to give credit where credit is due, but couldn't find an author. We were working on creating towers! Then we counted the levels (yes, our towers had to be on their sides), counted the pieces of steel (our steel looked like toothpicks), and worked on equations. The level of the tower was the Independent Variable, the 'steel' was the Dependent Variable, and the difference in every level was the coefficient.
|
AuthorWrite something about yourself. No need to be fancy, just an overview. Archives
September 2015
Categories |


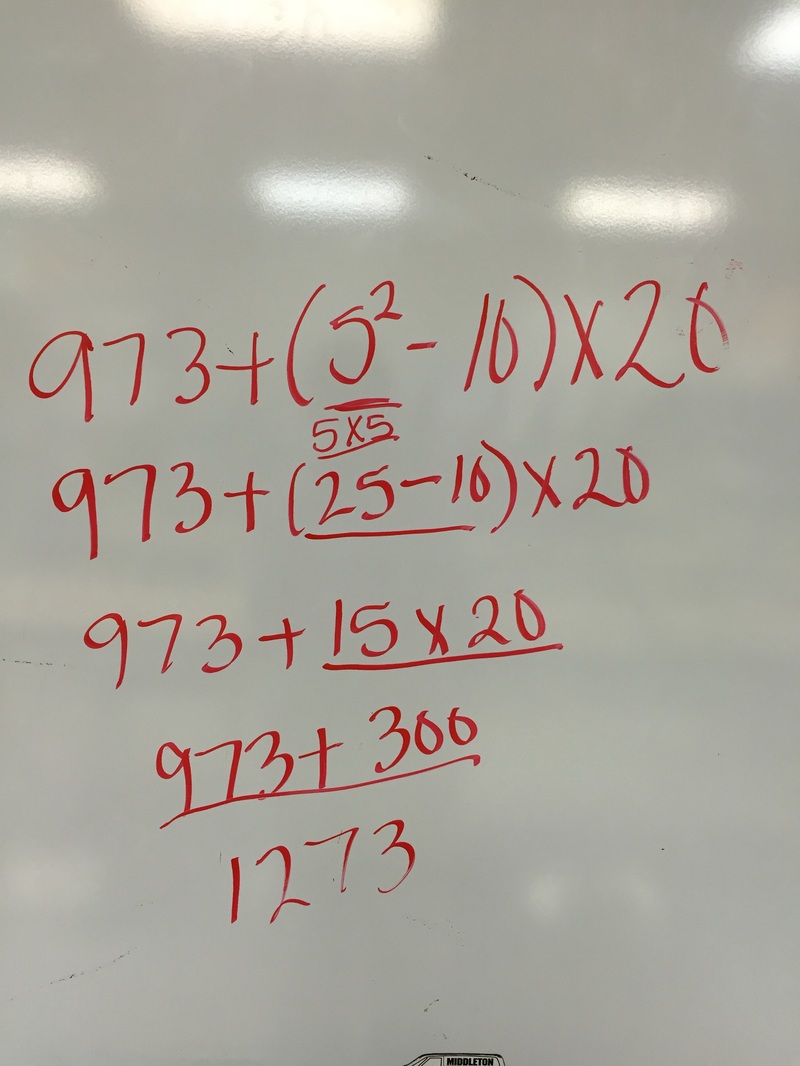





 RSS Feed
RSS Feed
